Panning and crossfade

The different panning laws

When positioning a sound source between two speakers (e.g. in a stereo image) we have to take care to preserve the perceieved loudness of the sound. We can use different panning algorithms (based on different panning laws) to do this. This issue in signal processing comes from the fact that the perceived loudness of a sound played on a single speaker is greater than the perceived loudness of the same sound played at half the original amplitude on two speakers simultaneously. Let us first state that there is really no single perfect solution, to a certain degree the choice of panning method is up to your own preference. We will now look at three different panning algorithms and listen to their differences. We have: Linear panning Square root panning *Sinusoidal panning We'll also talk about delay based panning later in this lesson.

Pan position

With all panning methods we will use a pan position value, signifying where we intend to put our sound source. The panning value we use have a range of 0.0 to 1.0, where a pan value of 0.0 puts the sound fully in the left speaker and a pan value of 1.0 puts it fully in the right speaker. A pan value of 0.5 should put the sound in the center of the stereo image. The problem, as stated above is to retain the same perceived loudness for the sound, regardless of the pan position.

Linear panning

In linear panning, the volume for each of the speakers change in a linear relationship to the pan position value. For the right speaker we simply set the volume equal to the pan value, and for the left speaker we invert the pan value (1-pan) and still retain a linear relationship. With this panning method, it sounds as if the sound has lower volume when panned to the center. This might be counter-intuitive, as we play the sound with 50% volume on the left speaker and 50% on the right speaker. Still, the two halves does not sum up to the same whole. If we wanted to preserve the same loudness of the sound, we would have to apply additional gain when it is panned between the speakers.

Noise panned left to right with linear panning

Audio sample panned left to right with linear panning

Square root panning

This method takes into account the fact the sounds panned to the center is perceived with lower loudness than sounds panned to the extreme left or right. For example, when the pan position is 0.5, the sum of amplitudes should be greater than 1, still we need to have the same amplitude on the left and right speakers for the soudn to be panned to the center. The square root panning method modify the volume for each channel by using the square root of the panning value as the gain factor for the right channel, and the square root of the inverted pan value as the gain factor for the left channel. This method works well, preserving the perceived loudness across the panning range. You may note the the relationship between panning position and perceived sound position is not neccessarily linear anymore. It sounds as if the sound moves quite quickly away from the left speaker when the pan position changes gradually from zero and upwards, then the sound movement becomes more slow in the center area, and speeding up again towards the right speaker. This may not be a big problem, as we generally adjust the panning parameter until our ears are satisfied with the result we hear. Still, it would be preferable to have a linear relationship between the panning value and the actual perceived sound position.

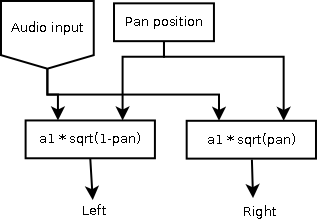
Noise panned left to right with square root panning

Audio sample panned left to right with square root panning

Sinusoidal panning

This method is similar to the square root panning in that it avoids the "hole in the middle" associated with linear panning. The difference from square root panning is the panning curve (the way the volume changes in relation to the pan position). Here, we use a sine function to calculate the gain factor for each speaker. For the left speaker we calculate the gain as sin(pan(pi/2)), and for the right speaker it is cos(pan(pi/2)). As with square root panning, this method also works well preserving the perceived loudness across the panning range. The relationship between panning position and perceived sound position is subtly different with sinusoidal panning than with square root panning. Many users would perceive this method as the one giving the smoothest movement when panning the sound, and the most linear relationship between pan value and perceived sound position.

Noise panned left to right with sinusoidal panning

Audio sample panned left to right with sinusoidal panning

Delay based pannning

As an extra tool for panning operations, we might also calculate the interaural time delay and use this to aid in creating realistic positioning of a sound source. This technique is particularly useful with headphone playback. Interaural means "between the ears", and the interaural time delay is the time it takes for a sound to travel the distance from one ear to the other. In a natural audio environment, sound waves from a source that is located to our left will reach our left ear before they reach our right ear. The time difference is small and can be calculated from the speed of sound and the distance between our ears. Consider that an approximate distance between our ear are 20 cm, and the speed of sound in dry air is approximately 340 meters per second. For sound to travel 1 meter, it takes 1/340 second (= 2,94 milliseconds). Then, for 20 cm it will take (1/340) * 0.2 m = 0,588 milliseconds, or approximately 0.6 milliseconds. As long as the delay time does not exceed this limit, our brain will try to decode the interaural delay as a positional cue. However, this technique is only effective for a certain frequency range (150Hz to 1500Hz). Low frequency signals are not easily located in any case, and the phase difference that results from interaural time delay is not significant for low frequencies. Signals with higher frequencies than 1500Hz will span more than one full wavelength in the distance available (20 sm), so the phase difference is not a reliable positional cue for these sounds. The subtle phase differences are also distorted somewhat when played back on speakers in a room, as the listener is seldom positioned at the exact sweet spot. For this reason it is most effective when used with headphones. With all these considerations, a significant portion of a normal sound still lies within the effective frequency range, and delay based panning can give added realism to a panning algorithm.

440 Hz sine wave delay panned left to right

Audio sample delay panned left to right

Crossfade

Many times when editing sounds, we want to apply a crossfade to mask the transition between different sound clips. When we look at perceived loudness, the same principle as we used for stereo panning applies here as well. When we crossfade between different sounds using a linear crossfade, the perceived loudness drops in the middle of the crossfade. Obviously, if we crossfade between two sounds that are identical, this principle does not apply. In all other cases it is good practice to apply a crossfade curve similar to the ones we used in our panning methods. Here are some sound examples of different crossfading curves: Linear crossfade Square root crossfade * Sinusoidal crossfade

Linear crossfade between two uncorrelated noise sources

Linear crossfade between two sample players (same sample with octave pitch change)

Square root crossfade between two uncorrelated noise sources

Square root crossfade between two sample players (same sample with octave pitch change)

Sinusoid crossfade between two uncorrelated noise sources

Sinusoid crossfade between two sample players (same sample with octave pitch change)