Bitreduction

Bitreduction is used as a technical means when converting between different sample bit depths, but is also commonly used as an effect for aesthetic purposes. Since the lower bit depth will represent the input signal with a lower numerical precision , we get a particular kind of distortion. Let's be very clear that it is the amplitude of the audio signal that is measured at each digital sample, and that the bit depth represents the precision with which the amplitude is measured.

Reducing the bit depth

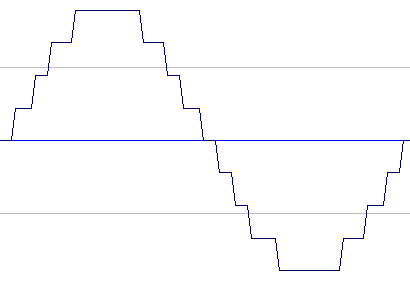
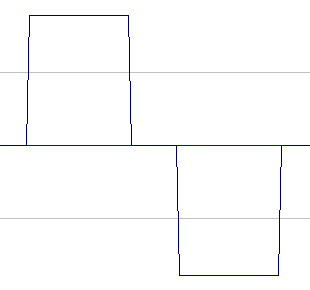
Here's we'll present an example of bitreduction by rounding off the sample amplitude value to a number of discrete steps. The number of steps is determined by the bit depth, for example a bit depth of 2 will allow 4 discrete amplitude steps while a bit depth of 8 allows 256 discrete steps. Just note that an audio signal is normally symmetrical around zero, and that what we think of as "audio signal zero" is indeed the middle value of the binary number representation. For 16 bits, we have 65536 discrete values, and to make this symmetrical around zero we use the first 32768 values to represent the negative signal amplitude and the other 32768 steps to represent the positive signal amplitude. Now, what do we do when the signal is silent? That is, when the amplitude is zero. Binary numeric representation tells us that zero is counted as a positive number so silent audio signal is registered as the value on the 32769'th step, leaving only 32767 steps for the positive part of the signal. This difference is negligible with high bit depths, but will really start to make a difference when using very low bith depths. So when we implement bit reduction as an audio processing effect, we must cheat one way or the other to preserve the signal symmetry around zero and to let zero represent the silent signal. The way we do this is to quantize the positive and the negative parts of the signal separately, leaving zero where it is. Now, this gives us another problem: how many steps can we allow for e.g. a 2 bit representation? 2 bits should give us 4 discrete steps, but we want to preserve zero as the middle value. So we just add zero as an extra allowed value, giving us 5 discrete steps for a 2 bit representation. This also let us do bit reduction to 1 bit, where the output will be very much like a square wave but still allowing a silent input signal to result in a silent output signal.

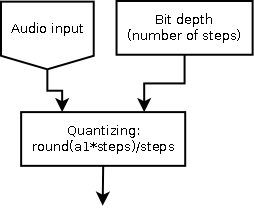
Signal Flow

Audio signal graphs

Sound examples

Csound code

The following Csound code generates a sine wave, then rounds off the amplitude values to the agreed number of steps.

;***************************************************
; bit reduction
;***************************************************
	instr	1

; basic parameters: amp and frequency for the oscillator
	iamp		= ampdbfs(p4)
	icps		= p5

; bit depth
	iBits		= p6				

; find number of discrete steps for this bit depth
	iQuantize	= (powoftwo(iBits)/2)+1		

; audio generator
	a1		oscili	1, icps, giSine	

; bit reduction by rounding off amplitude values
	aQuantize	= round(a1*iQuantize)/iQuantize	

; audio out
	out		aQuantize*iamp		

	endin
;***************************************************